30 60 90 Triangle Ratio, Formula & Sides
The 30-60-90 triangle is a special right triangle widely used in trigonometry because it has well-defined relationships between its angles and sides, which can be used to calculate trigonometric functions such as sine, cosine, tangent, and cotangent.
Also known as a “half equilateral triangle,” it gets its name from the fact that if you draw an equilateral triangle and draw an altitude to one of its sides, you will create two 30-60-90 triangles.
30-60-90 triangle rule
Among all the rules, the 30 60 90 triangle rule holds a significant place in geometry. It is valuable in geometry and trigonometry because of its predictable ratios between the lengths of its sides, which can be utilized to solve for unknown values.
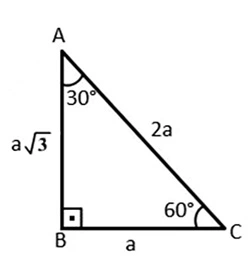
The side lengths of this triangle adhere to a specific ratio. The lengths of the sides of a 30-60-90 triangle can be summarized as having a particular relationship, as follows.

- The length of the hypotenuse is twice the length of the side opposite the 30-degree angle.
- The length of the side opposite the 60-degree angle is √3 times the length of the side opposite the 30-degree angle.
- We will always consider the length of the side opposite the 30-degree angle as the starting point because the transition from small to large is easier.
Shortest side = a
Longer side = a√3
Hypotenuse = 2a
Just knowing these ratios will allow us to analyze and practice problem-solving. Therefore, let’s keep these ratios in mind. The values we need to know are 1, √3, and 2.
Example;
In a right triangle, if the length of the side opposite the 30-degree angle is 6 cm, what are the lengths of the other sides?
The hypotenuse is twice the length of the side opposite the 30-degree angle, so it is 2 * 6 = 12 cm.
The side opposite the 60-degree angle is √3 times the length of the side opposite the 30-degree angle, so it is 6 * √3 = 6√3 cm. Alternatively, since it is (√3)/2 times the length of the hypotenuse, it is again 12 * (√3)/2 = 6√3 cm.
Therefore, the sides of this 30-60-90 triangle are 6 cm, 6√3 cm, and 12 cm.
We can extend the examples of the 30-60-90 triangle. You can find 30-60-90 triangle questions and answers in the “Right Triangles” category under triangle tests.
In conclusion, if you know the length of one side, you can use these ratios to find the lengths of the other two sides.
If we know the lengths of any two sides…
Yes, we can use these ratios again to find the length of the third side. Alternatively, we can use the Pythagorean theorem, which states that in a right triangle, the sum of the squares of the two legs is equal to the square of the hypotenuse.
We know the ratios, but we got confused about whether it was √3 times the side opposite the 30-degree angle or the side opposite the 60-degree angle…
What should we do?
Let’s draw the 30-60-90 triangle.
Immediately, we write down “1” for the length of the side opposite the 30-degree angle because it is the shortest side.
Then, we ask ourselves if it’s 2 or √3. If √3 were equal to √4, we would take the value of 2, so we say it’s 2…
Since 2 is the largest, we can write “2” for the side opposite the 90-degree angle, and consequently, “√3” for the third side, which is the side opposite the 60-degree angle.
But what if we don’t know the rule…?
The Significance of Sin(30) Value in the 30-60-90 Triangle
We will examine the importance of the Sin(30) value in determining the ratios between the short side, long side, and hypotenuse in the 30-60-90 triangle. Trigonometry emerges as a branch that plays an important role in geometry and mathematics. Particularly, the use of trigonometric functions in triangles allows us to understand the relationship between angles and side lengths.
The sine function represents the ratio of the side opposite an angle to the hypotenuse. The value of Sin(30) holds significance in the analysis of special triangles like the 30-60-90 triangle and in geometric calculations. This is where Sin(30) comes into play.
The value of the sine of the 30-degree angle, mathematically expressed as Sin(30), is equal to 1/2. This means that the short side will be half the length of the hypotenuse.
Therefore, in the 30-60-90 triangle, the length of the hypotenuse is twice the length of the side opposite the 30-degree angle.
In conclusion, it demonstrates the significant role of trigonometric functions, specifically sine values, in determining the ratios in the lengths of the sides of a triangle.
Let’s draw a 30°-60°-90° triangle.
Since sin30° is equal to the ratio of the side opposite the angle to the hypotenuse, we can determine the ratio between the side opposite the 30° angle and the hypotenuse as 1:2. As for the side opposite the 60° angle, we can determine its ratio by either using sin60° or the Pythagorean theorem, which would be √3.
Here, in the 30-60-90 triangle, the most important thing is to either know the rule or apply the trigonometric function.
But what if we have no idea…
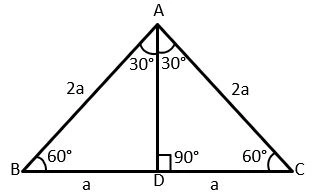
In an equilateral triangle, we draw a perpendicular to any side. Since the perpendicular acts as the median, angle bisector, and altitude, it divides the side into two equal lengths. Therefore, we observe a ratio of 1:2. By using the Pythagorean theorem, we can also determine that the third side has the ratios of Shortest side = a, Longer side = a√3, Hypotenuse = 2a in the 30-60-90 triangle..
The properties and applications of the 30-60-90 triangle make it a valuable tool in solving geometric problems and designing real-world structures. It finds practical applications in fields such as engineering, architecture, and construction. For example, it can be used to design and construct ramps, stairs, and other structures with gradual slopes.